虛擬資產:如何利用門限簽名來生成隨機信標？

作者:?ALEXANDERSKIDANOV

翻譯&校對:?IANLIU?&阿劍

來源：以太坊愛好者

回顧2015，DFinity項目提出了令整個社區都為之興奮的隨機信標方案——使用BLS門限簽名產生隨機輸出，同時保證輸出的無偏性及不可預測性。然而，時至2020年的今天，構建無偏且不可預測的隨機信標仍然困難重重，還在研究的項目少之又少。

其實門限簽名只是構建隨機信標的可行方法之一，我們前面發表過一篇概覽文章，介紹其他可能的解決方法，其中包含本文要重點提到的一種。其他細節——隨機信標是什么？什么是無偏性及不可預測性？除了門限簽名還有什么方法——這些問題都能在上述概覽中得到解答。

經過了多次設計迭代，我們最終提出類似DFinity的方案，這也是我們進一步深入理解隨機信標的大好契機。

本文將以淺顯的形式，講述門限簽名生成隨機數的一系列協議。

密碼學基礎知識

為了更好地了解本文中提到的隨機信標，我們需要掌握一些基礎密碼學知識。首先，我們必須區分兩個概念：1.在本文中以小寫字母表示標量，或者說普通常量；2.用大寫字母表示橢圓曲線上的點。

我們不需要對橢圓曲線點了解得很透徹，只要掌握下面兩點：

陳茂波：如何將虛擬資產服務提供者納入合適規管是特區政府的重點所在:金色財經報道，香港財政司司長陳茂波接受《大公報》最新訪問時提到虛擬資產發展，特區政府去年發表有關虛擬資產在港發展的政策宣言，闡明政府為在香港發展具活力的虛擬資產行業和生態系統而訂定的政策立場和方針，近期亦積極推動Web3生態圈發展。陳茂波表示，如何將虛擬資產服務提供者納入合適規管，保護投資者利益，同時又保持金融穩定和安全，是特區政府的重點所在。[2023/6/23 21:56:03]

1、橢圓曲線點可以相加，也可以跟標量相乘，然后得到另一個橢圓曲線點。

2、即使知道G和xG的值，也不可能計算出x的值。

在本文中，我們還將用到k-1階多項式p(x)；關于p(x），你不用想太多，只要把它當成一個方程就好，而且：只要你知道在k個不同的x下p(x)的值，你就能推導出所有x的p(x)值。

以此類推，對于同一個函數p(x)和基點G，如果你知道p(x)G代入k個不同的x值后的值，就可以推導出所有x所對應的p(x)G值。

只要明白了有關橢圓曲線點的這些屬性，就能深度理解隨機信標的工作原理了。

隨機信標

假設1：系統中有n個參與者，至少需要其中的k位才能產生隨機數。就算控制其中的k-1人，你也不能預知隨機信標的輸出結果、無法操縱結果。

墨西哥官員會見Samson Mow討論墨西哥如何采用Bitcoin:金色財經報道，Bitcoin Magazine在社交媒體上發文表示，墨西哥參議員兼財政部委員會主席會見Samson Mow討論墨西哥如何采用Bitcoin。[2023/4/30 14:35:25]

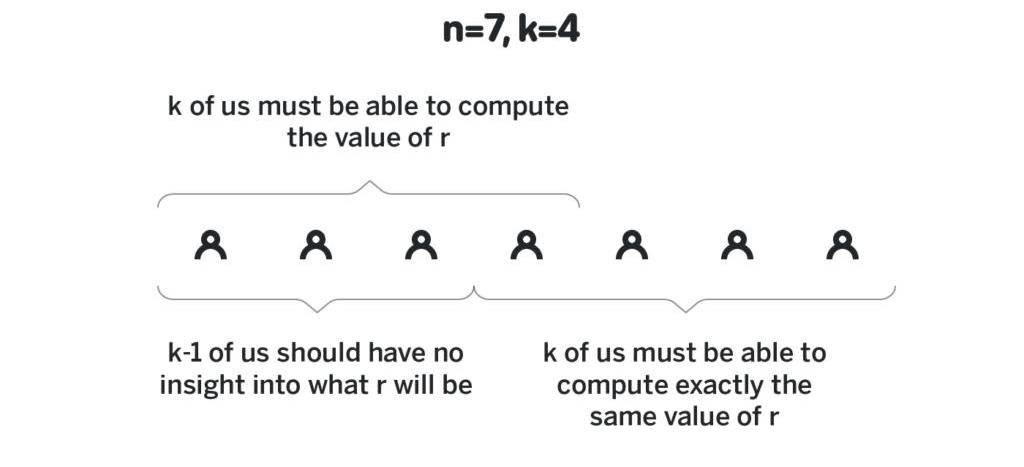
假設2：現在有個k-1階多項式p(x)，參與者1知道p(1)的值、參與者2知道p(2)的值、……、參與者n知道p(n)的值；大家約好使用G作為橢圓曲線基點，所有參與者都知道p(x)G代入所有x的值。我們將p(i)視為參與者i的“私人份額”，而p(i)G是其“公開份額”

要設計好的隨機信標，最困難的部分，就是要找到這么一個多項式，使得每個參與者都能知道自己的私人份額，但是無法知道他人的私人份額——這也被稱為分布式密鑰生成。DKG會放在下個章節討論，現在就先假設存在這么個多項式，而所有人都知道各自的私人份額。

我們接著討論，如何使用這套假設在區塊鏈協議中產生一個隨機信標？假設網絡產生一個區塊，區塊哈希為h。現在參與者們想用h作為種子以生成隨機數，首先用約定好的函數，將h轉換為某條橢圓曲線上的一個點：

H=scalarToPoint(h)

DFI.Money（YFII）發起關于如何分配Balancer獎勵提案:9月3日，聚合器項目DFI.Money（YFII）收到首批Balancer（BAL）獎勵，共計BAL 679.83個，價值21,814美元。該獎勵來源于YFII/DAI礦池，后續每周都將收到。關于獎勵如何分配，社區發起提案進行投票：放進循環挖礦池；換成yCRV給投票人激勵參與投票；注入社區基金。[2020/9/8]

對于參與者i來說，因為他知道p(i)和H，所以可以自行計算出H_i=p(i)H。對外公布H_i并不會導致參與者i的私人份額p(i)暴露，因此在每個區塊中都能重用同樣的私人份額，因此DKG只需要進行一次。

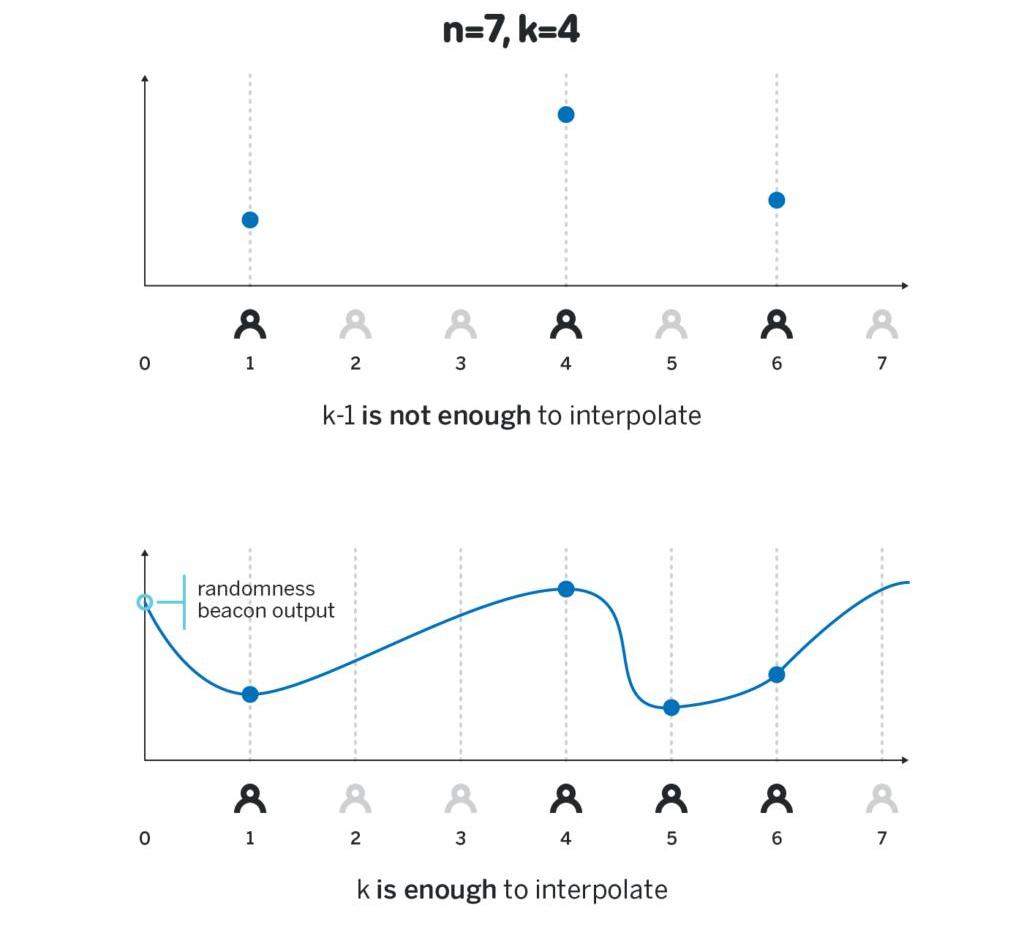
根據前面提到的第三點特性，當至少有k位參與者公布他們各自的H_i=p(i)H之后，其他人就能知道代入任何一個x之后，H_x=p(x)H是什么。然后所有參與者都可以在自己本地計算H_0=p(0)H，并以這個結果的哈希值作為隨機信標的輸出；請注意，因為沒有參與者知道p(0)，所以唯一能得到p(0)H的方法就是對p(x)H進行內插法計算，要完成內插計算需要知道至少k個p(i)H的值。如果公布的人不足k位，則其他人無法推出p(0)H的值。

復旦大學教授許多奇：當今國際社會首當其沖的問題是如何判定數字貨幣法律性質:日前在金融法治菁英論壇上，復旦大學法學院教授許多奇表示，如何監管加密數字貨幣是當今國際社會普遍關注的問題，而首當其沖的問題是加密數字貨幣的法律性質判定問題，司法機關有關加密數字貨幣屬性的判定能否成為實現有效監管的基礎？在眾多司法轄區的多種監管思路中我們應作何種選擇？對于這些問題的思考和深入研究對于實現對加密數字貨幣的有效監管大有裨益。（中國貿易報）[2020/4/29]

基于此技術構建的信標延續了這些我們所需的特性：如果攻擊者只掌控了少于k-1位參與者，則他無法操控隨機信標的輸出；其他k位參與者才能計算出最終輸出，他們的子集或其他更多的參與者，都能得出相同的輸出。

我們還忽略了一件事。為了使用插值法計算p(0)H，必須保證參與者i所公開的H_i真的等于p(i)H。但是因為除了參與者i，其他參與者都不知道p(i)是什么，所以沒法直接驗證參與者i公布的H_i是否的確等于p(i)H；如果不要求為H_i附上密碼學證明，攻擊者可以直接聲稱某個H_i的值，而其他人沒有辦法辨別真偽。

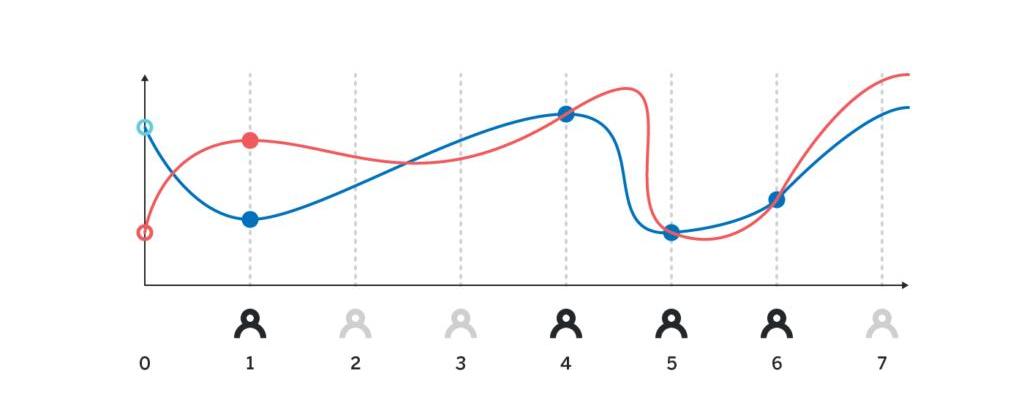
有至少兩種密碼學證明辦法，可以用來判別H_i的真偽。我們會在聊完DKG之后介紹。

大咖零距離 | 如何使用火箭戰法2天盈利20倍:3月19日18:00，金色盤面邀請實盤大V莊見愁做客金色財經《大咖零距離》直播間，將分享《如何使用火箭戰法2天盈利20倍》，敬請關注，欲進群觀看直播掃描海報二維碼報名即可！[2020/3/19]

分布式密鑰生成

根據前面章節對隨機信標的介紹，我們需要n位參與者共同使用某個k-1階多項式p(x)，使得每個參與者i知道自己的p(i)，而其他人無法得知。下一步，需要所有參與者都知道：給定G時，所有的x所對應的p(x)g值。

在本章節，我們假設每個人都有自己的私鑰x_i，而且其他人都知道x_i對應的公鑰X_i。

那么運行DKG的一種方式如下：

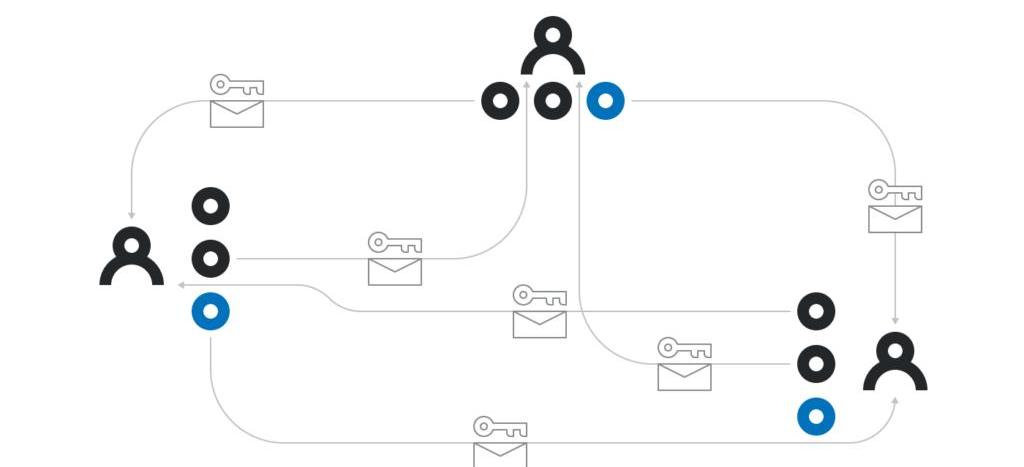
1、每個參與者i在本地運行k-1階多項式p_i(x)的計算。接著用公鑰X_j將每個p_i(j)加密，并發送給對應的參與者j。如此一來，只有參與者j能解密出p_i(j)；參與者i還要公布所有p_i(j)G，j∈1~k。

2、所有參與者要對一個至少由k個多項式組成的集合達成共識。因為有些參與者可能掉線，所以他們不可能等到n個驗證者都作出如此承諾再進行下一步；只要至少k個驗證者都作出“收到至少k個這樣的多項式”的承諾之后，他們就可以使用某種形式的共識算法對他們所收到多項式的子集Z達成共識。

3、所有參與者共同驗證加密的p_i(j)與公開的p_i(j)G是否對應，并從Z中移除不合格的多項式。

4、對于集合Z中的每個多項式p_i(x)，每個參與者j自行計算p_i(j)的總和作為私人份額p(j)；同樣的，對于集合Z中的每個p_i(x)G?，參與者可以計算p_i(x)G的總和作為公開份額p(x)G。

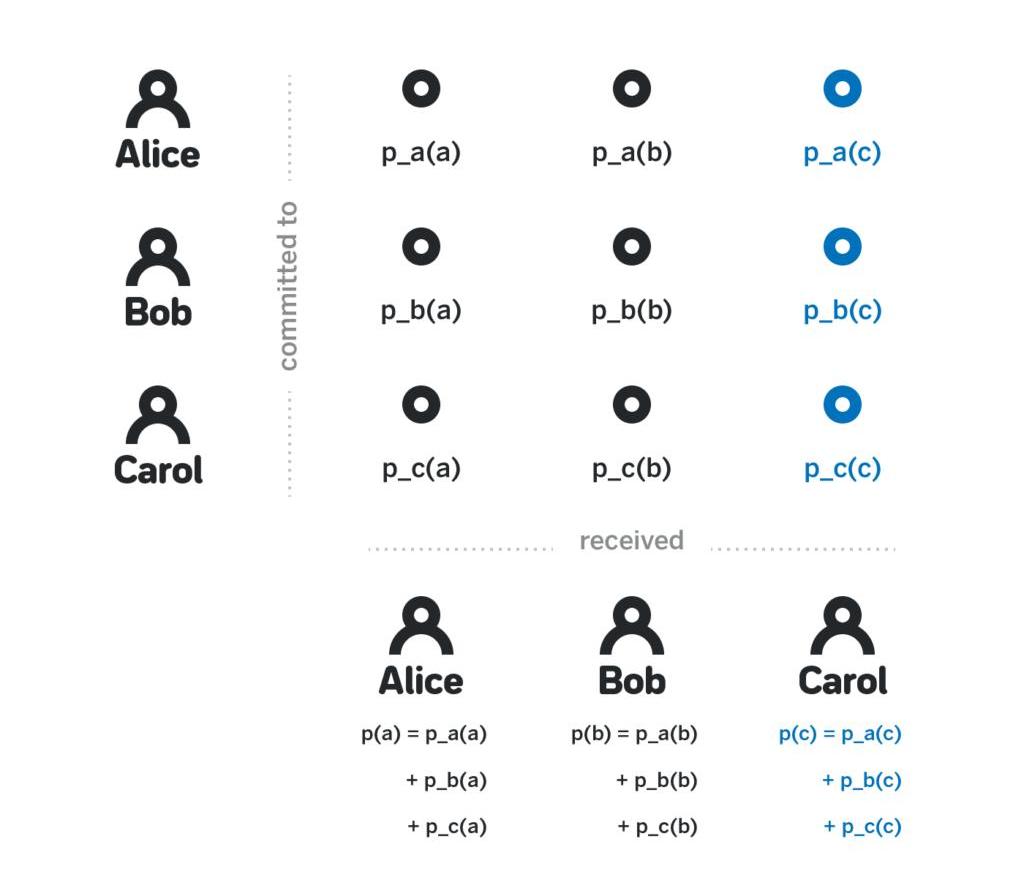
因為p(x)是每個獨立的p_i(x)的總和，每個p_i(x)都是k-1階多項式，所以要觀察p(x)是否也是k-1階多項式。其次要注意，每個參與者j只知道p(j)的值，但不知道其他p(x)的值。實際上，為了知道p(x）的值，TA需要知道所有的p_i(x），只要至少一個被承諾多項式的值屬于未知，TA就不可能知道p(x)。

上述步驟組成了完整的DKG過程。步驟1、2、4相對直觀，但第3步就比較復雜了。

具體來解釋第三步——我們需要找個方法，證明每個加密的p_i(j)與公開的p_i(j)G存在對應關系。如果沒有這種驗證，攻擊者i可以向參與者j胡亂發送消息，而不是發送正確的加密p_i(j)，導致參與者j無法進一步計算自己的私人份額。

雖然有辦法可以制作出加密份額的形式正確性密碼學證明。但是，這樣的證明數據過大，并且要向全網公布這樣的證明，時間復雜度可能高達O(nk)，證明的size是嚴重的瓶頸。

在NEAR協議中，我們不去證明p_i(j)與公開的p_i(j)G的關系，而是在DKG過程中給予每個參與者充分的時間，去證明“他們收到的p_i(j)與公開廣播的p_i(j)G對不上”。協議中假設每個參與者在窗口期內至少會上線一次，而他們提交的挑戰就能進入區塊鏈。對于區塊生產者來說，這兩個假設都很合理，因為要做區塊生產者，一般來說在整個epoch中都要在線；如果大多數區塊生產者密謀不接收這條消息，其實整個系統就已經不安全，攻擊者其實有更好的方式攻擊整個系統。

假如某個區塊生產者收到無效的公開份額，而且沒有及時在DKG過程中提出挑戰，則該礦工也無法在該時段中參與隨機數生成。請注意，只要其他k個誠實的參與者都能正確計算出份額，協議仍將正常運作。

證明

還剩下最后一個問題：我們如何以不透露p(i)為前提，證明自己公布的H_i等于p(i)H？

回想一下，每個參與者都知道H、G、p(i)G的值。在給定p(i)G和G的情況下回推p(i)的運算被稱為離散對數問題，又簡稱為dlog。那么每個參與者想做的都是：既能向他人證明?dlog(p(i)G,G)=dlog(H_i,H)，又不會透露p(i)。的確存在這么一種方法構建上述證明，其中之一就是——Schnorr協議；通過Schnorr協議，參與者能在發布H_i時附上H_i的正確性證明。

回想一下，隨機信標連的輸出是H_0的內插值。對于沒有參與生成隨機信標輸出的人來說，除了H_0，還需要哪些信息來驗證這個值的正確性？因為每個人都能自行在本地計算中加入G_0，所以只要證明?dlog(G_0,G)=dlog(H_0,H)?就行了。但因為信標的特性，我們無法得知p(0)，也就無法通過Schnorr協議生成這樣的證明。所以如果你要向其他人證明H_0的正確性，就必須保留所有H_i的值及其相應的證明。

不過，好消息是，如果有些計算類似于橢圓曲線點乘法，則只需驗證?H_0×G=G_0×H?即可證明H_0的計算正確無誤。

如果所選的橢圓曲線支持橢圓曲線配對運算，則這種證明是可行的。在這種情況下，任何知道G，H和G_0的人都可以核實H_0；而且H_0也可視作一個集體的多重簽名，證明區塊n的正確性得到至少k位參與者的檢查認證。

目前我們還未在NEAR中使用橢圓曲線配對運算，但未來我們可能會使用，然后利用上文討論的小技巧取代我們當前使用的單一簽名方法。另一方面，DFinity使用BLS簽名，可以利用配對運算來實現上述簽名。

原文鏈接：https://nearprotocol.com/blog/randomness-threshold-signatures/

Tags：DLODFI虛擬資產數字貨幣DLO價格StakedFIRO虛擬資產驗證后京東支付無需再驗證數字貨幣交易員工作咋樣

中幣下載