比特幣:密碼學原語如何應用？解析密碼學承諾的妙用

作者：廖飛強?

來源：微眾銀行區塊鏈

在不泄露明文的前提下，如何對隱私數據的內容進行承諾？密碼學承諾的密文形式和普通的數據密文有何區別？隱私數據如何在密碼學承諾的形式下依舊保持可用性？在量子計算的安全模型下，是否依舊可以構造安全可用的密碼學承諾？

隱私保護方案設計中，除了保護隱私數據的機密性，確保密文形式隱私數據解讀的唯一性也是重要的業務需求。業務流程中，很大程度會依賴隱私數據的具體數值，如果允許攻擊者在自身利益驅動下，對處于密文形式的隱私數據進行任意解讀，勢必會對業務的整體公正性和有效性帶來巨大影響。

以電子支付為例，一家銀行為一位客戶開具了一張面額1000元的電子支票，電子支票以密文形式交付給客戶，流轉過程中不會輕易泄露金額。然而，在使用時，銀行也不希望客戶能夠將這張電子支票解讀成其他金額，如10000元。多兌現的9000元會造成銀行的損失，銀行甚至可能因此而停用整個密文電子支票業務。

這里的解讀與解密有一定區別，對密文數據解讀不一定需要對密文數據進行解密。在上面示例中，當客戶花費這張面額1000元的電子支票，解讀時只需要證明電子支票的消費額小于未花費余額即可，而不需要解密未花費余額的具體數值。

解決以上業務問題的關鍵，就在于密碼學承諾的使用。密碼學承諾有何神奇之處？且隨本文一探究竟。

密碼學博士高承實：量子計算機大規模應用將對非對稱密碼算法和哈希函數帶來致命性的影響:密碼學博士，計算機應用專業副教授高承實發表《量子計算機的應用會顛覆掉比特幣系統嗎？》專欄文章，文章表示，量子計算機從發展狀況來看，還處于極其早期階段，離真正實用還有相當遠的距離。如果量子計算機真正能夠大規模應用，將對密碼算法當中的非對稱密碼算法和哈希函數帶來致命性的影響。現在基于數學難解問題而生成的非對稱密碼算法RSA和ECC安全性將不復存在，哈希函數的抗碰撞性也將受到極大挑戰，除非盡可能增加哈希函數的輸出長度。目前的非對稱密碼，主要是ECDSA和哈希函數SHA256，是比特幣系統最核心的底層技術，確保了比特幣分配和支付的安全，在比特幣系統的多個環節得到了應用，包括生成錢包地址、對交易進行簽名和驗證、計算區塊內所有交易的默克爾數生成區塊以保證塊內數據難以被篡改、激勵礦工開展挖礦競賽以維護系統的自運行……如果ECDSA和SHA256兩種算法的安全性不復存在，那么整個比特幣系統的安全性也將不復存在。

當然我們也沒有必要那么悲觀。第一，量子計算機的真正使用還有相當遠的距離；第二，隨著量子計算以及量子計算機的發展，抗量子計算的密碼算法也會同步得到發展，比如格密碼。

真的到了那個時候，或者比特幣系統中的密碼模塊會替換為抗量子計算的密碼模塊，或者比特幣已經完成它的歷史使命，從這個世界上消亡。（財新）[2020/12/24 16:21:46]

1.哈希承諾

V神發推預測21世紀20年代密碼學大趨勢:金色財經報道，V神今日在推特上表示：2010年代密碼學的大趨勢是橢圓曲線、配對和通用ZKPs/SNARK；預測21世紀20年代的大趨勢將是（除了廣泛采用上述技術外）格（lattices）、LWE、多線性映射、同態加密、MPC和模糊處理。[2020/4/11]

在日常生活中，承諾無處不在。例如，預約打車成功后，司機和乘客之間就互相做了一個承諾。到了預約時間，乘客等車，司機接客，這就是在兌現承諾。

信息科學中也有類似的承諾技術存在。例如，某些網站在提供下載文件時，也會提供對應文件的單向哈希值。這里，單向哈希值便是一種對文件數據的承諾，以下稱之為哈希承諾。基于下載的哈希承諾，用戶可以對下載文件數據進行校驗，檢測接收到的文件數據是否有丟失或變化，如果校驗通過，相當于網站兌現了關于文件數據完整性的承諾。

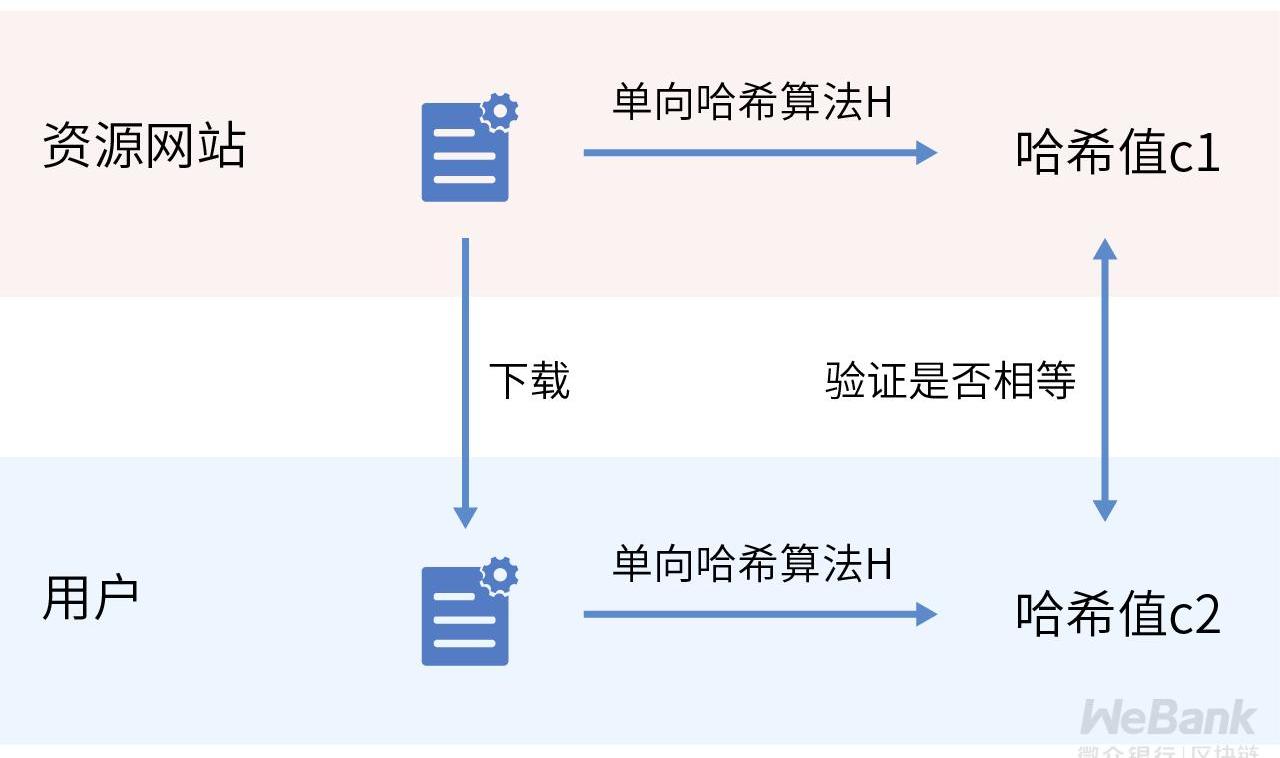
密碼學承諾是一類重要的密碼學原語，其中哈希承諾又是諸多技術中最簡單的一種實現方式。

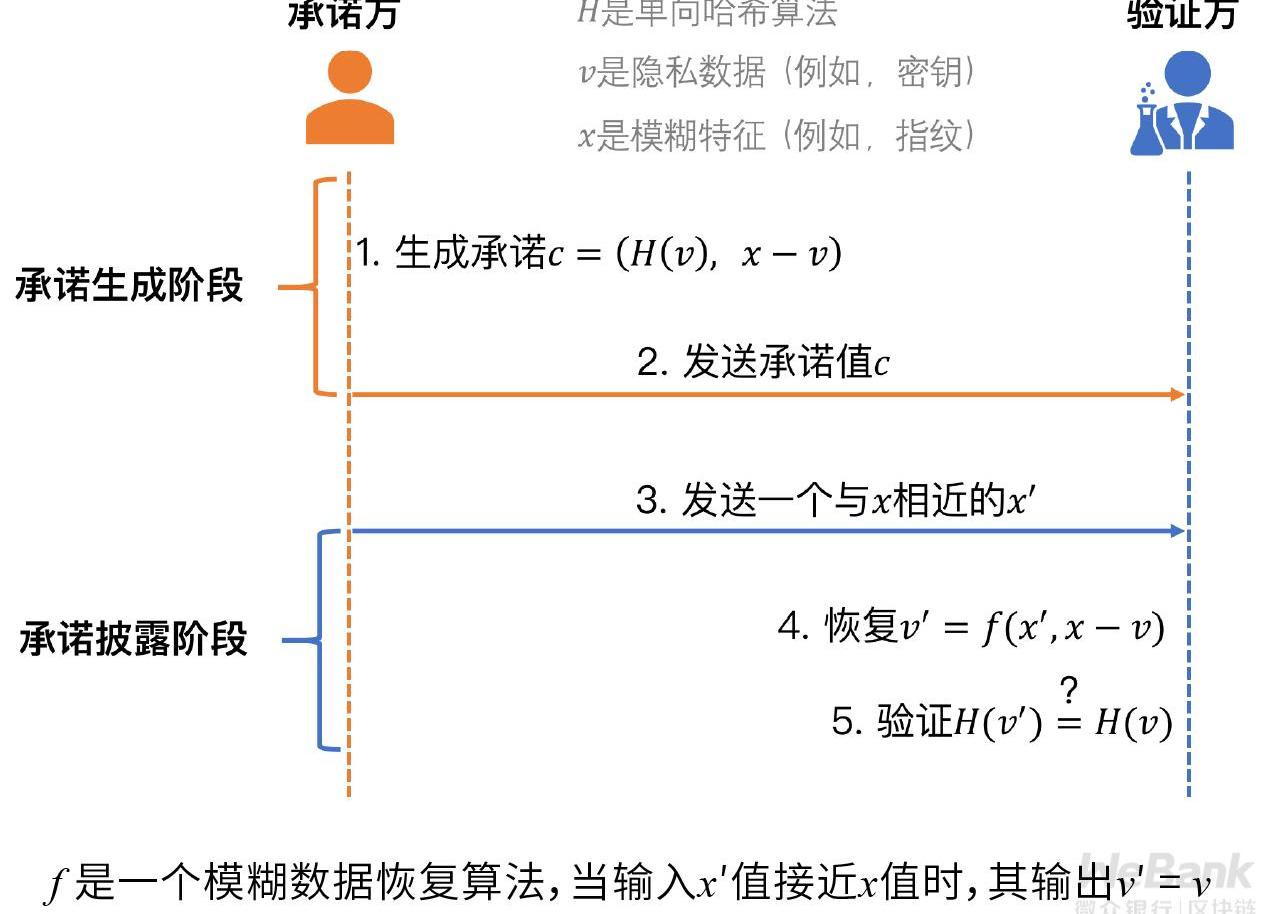
一般而言，密碼學承諾的應用涉及承諾方、驗證方兩個參與方，以及以下兩個使用階段。

第一階段為承諾生成階段，承諾方選擇一個敏感數據v，計算出對應的承諾c，然后將承諾c發送給驗證方。通過承諾c，驗證方確定承諾方對于還未解密的敏感數據v只能有唯一的解讀方式，無法違約。

聲音 | Anchorage聯合創始人：加密技術正在開創分布式系統、安全性和密碼學研究的新領域:據AMBCrypto報道，在最近的一次演講中，加密安全公司Anchorage的聯合創始人Diogo Monica談到了加密在提高個人安全、隱私和數據主權方面的作用。Diogo注意到加密降低了黑客攻擊和服務中斷的風險，他宣稱加密技術正在開創分布式系統、安全性和密碼學研究的新領域。他稱，“缺乏個人安全、缺乏隱私和數據主權是我們日常生活中的事情，我們接受這些東西作為互聯網的一部分，但這不應該是這樣，這就是加密技術的來源。加密貨幣的發展實際上幫助你的每一臺設備變得更安全，因此有助于你的個人安全，新的加密方法有助于保護你的數據，并最終讓你重新獲得一些隱私。”[2020/2/3]

第二階段為承諾披露階段，學術界通常也稱之為承諾打開-驗證階段。承諾方公布敏感數據v的明文和其他的相關參數，驗證方重復承諾生成的計算過程，比較新生成的承諾與之前接收到的承諾c是否一致，一致則表示驗證成功，否則失敗。

一個設計良好的密碼學承諾具備如下特性：

隱匿性：在打開關于v的承諾c之前，驗證方不知道承諾方選擇的敏感數據v。

綁定性：在關于v的承諾c生成之后，承諾方難以將已承諾的敏感數據解釋成另一個不同的數據v'。

所以，密碼學承諾可以起到與日常生活中的承諾行為類似的效果，一旦做出承諾，就必須在披露階段使用之前已經承諾的敏感數據。

動態 | 谷歌將采用密碼學以保持數據集的私密性:據wired報道，谷歌將發布一個名為Private Join and Compute的開源加密工具。它有助于連接來自不同數據集的數字列，以計算在整個數學過程中加密和不可讀數據的總和，計數或平均值。只有計算結果才能被所有各方解密和查看 - 這意味著你只能獲得結果，而不能獲得你未擁有的數據。該工具的加密原理可以追溯到20世紀70年代和90年代，但谷歌已經重新利用并更新它們，以便與當今功能更強大、更靈活的處理器配合使用。[2019/6/21]

對應地，在業務系統中，承諾生成階段通常被用來生成密文形式的業務數據，而承諾披露階段則多被用于在特定業務流程中進行數據校驗。

除了直接公布敏感數據明文之外，承諾披露階段所需的數據校驗，也可以在不公布敏感數據明文的前提下，構造零知識證明來完成。相關內容將在后續零知識證明專題中展開。

具體回到哈希承諾，用戶可以通過以下公式計算關于敏感數據v的承諾，其中H是一個密碼學安全的單向哈希算法。

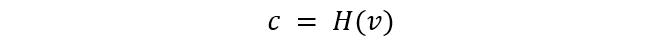
基于單向哈希的單向性，難以通過哈希值H(v)反推出敏感數據v，以此提供了一定的隱匿性；基于單向哈希的抗碰撞性，難以找到不同的敏感數據v'產生相同的哈希值H(v)，以此提供了一定的綁定性。

聲音 | 肖風：密碼學已在理論上有很多成果可供解決數據隱私保護問題:今日在“Web 3.0時代隱私計算構建新數據共享世界”峰會上，萬向區塊鏈董事長肖風表示，隨著人工智能的興起，隱私計算成為世界性話題。然而，并非所有數據都存在于互聯網平臺上，也不是所有數據都是法律法規允許共享的。因此隱私計算的概念才得以提出，而恰恰密碼學已在理論上有很多成果可供我們來探討解決數據隱私保護問題。[2018/12/1]

哈希承諾的構造簡單、使用方便，滿足密碼學承諾基本的特性，適用于對隱私數據機密性要求不高的應用場景。

對隱私數據機密性要求高的應用，需要注意哈希承諾提供的隱匿性比較有限，不具備隨機性。對于同一個敏感數據v，H(v)值總是固定的，因此可以通過暴力窮舉，列舉所有可能的v值，來反推出H(v)中實際承諾的v。

相比其他密碼學承諾技術，哈希承諾不具有便于業務系統在密文形式對其處理的附加功能，例如，多個相關的承諾值之間密文運算和交叉驗證，對于構造復雜密碼學協議和安全多方計算方案的作用比較有限。

2.Pedersen承諾

Pedersen承諾是目前隱私保護方案中使用廣泛的密碼學承諾，相比哈希承諾，構造略微復雜，但提供了一系列優異的特性：

信息論安全（參見

第4論）的理論最強隱匿性。

基于離散對數困難問題（參見

第3論）的強綁定性。

具有同態加法特性的密文形式。

其具體構造如下：

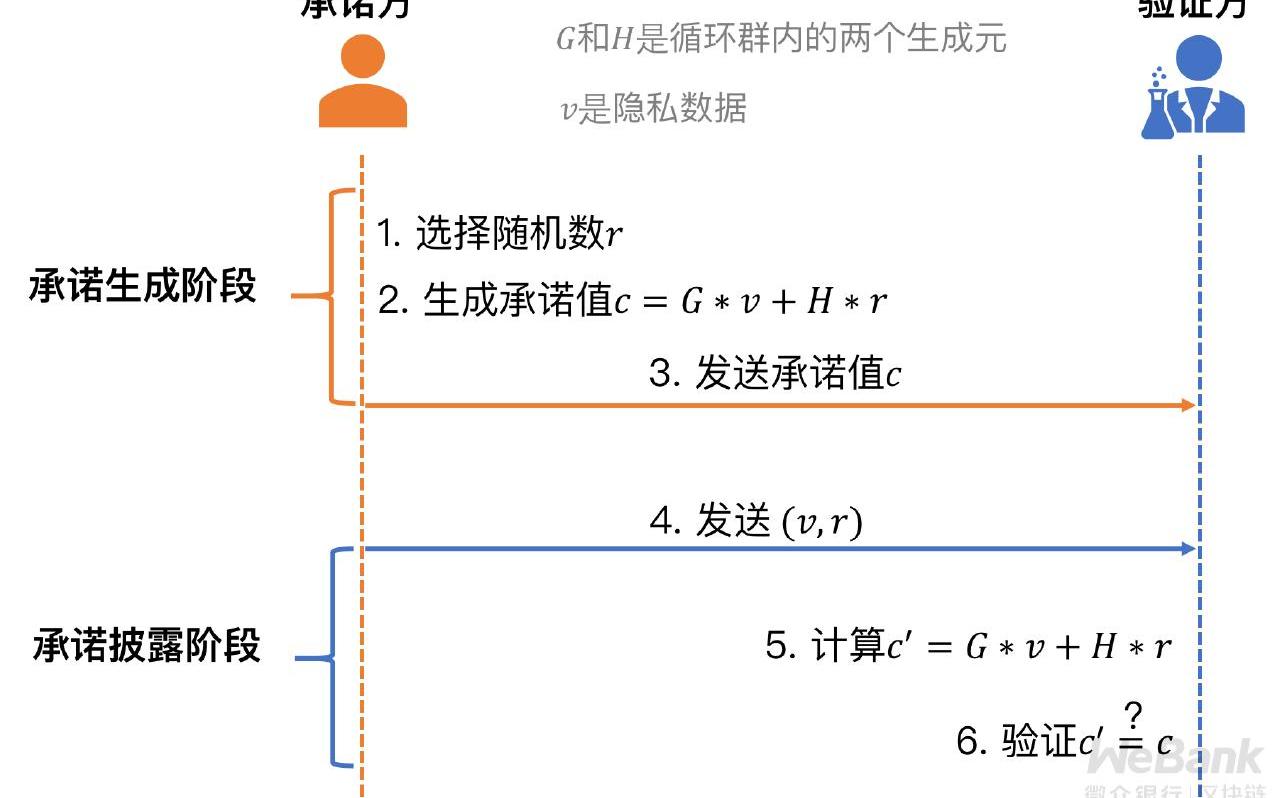
有別于哈希承諾，對于同一個v會產生相同的承諾H(v)，Pedersen承諾通過引入隨機致盲因子r，即便隱私數據v不變，最終的承諾c也會隨著r的變化而變化，以此提供了信息論安全的隱匿性。

Pedersen承諾在構造中采用了離散對數運算，因此也賦予其加法同態性。可以通過兩個分別關于v1和v2的Pedersen承諾c1和c2“相加”，得到的新承諾便是關于v1+v2的Pedersen承諾。

除了能夠構造關于v1+v2的Pedersen承諾之外，Pedersen承諾還可以用來構造v1*v2、v1||v2等更復雜的Pedersen承諾，通過基于離散對數的通用零知識證明系統，來證明新產生的承諾滿足與原始承諾c1和c2之間存在指定的約束關系。

在實際業務中，Pedersen承諾自帶的加法同態性，配合零知識證明獲得約束關系證明功能，在區塊鏈中可以有廣泛的應用，目前主要以隱匿賬本的形式，提供靈活的隱私數據的密文上鏈存證和交易密文數值關聯性的第三方驗證。

具體方案設計中，相關業務方在鏈下完成業務交互之后，將對應的數值變化表達成Pedersen承諾，再將對應的承諾數據上鏈，這個過程中無需披露任何隱私數據明文。

上鏈之后，非相關的第三方雖然難以通過Pedersen承諾的密文形式反推出隱私數據明文，但可以驗證承諾之間的約束關系，核實業務交互的合法性，例如，驗證隱匿轉賬發生之后，依舊滿足會計平衡、外匯交易中使用了正確匯率進行跨行對賬等。

值得注意的是，Pedersen承諾產生的密文形式，與通過普通加解密算法生成的數據密文有一定相似性，在計算過程中都使用敏感數據v，致盲因子r的作用和密鑰的作用也有一些相似，均用以混淆最后的密文輸出。

但不同的是，密碼學承諾不提供解密算法，如果只有r，無法有效地提取出敏感數據v的明文，只能通過暴力窮舉所有可能的v值的方法逐一驗證，試圖通過匹配的承諾值來破解v的明文。

所以，Pedersen承諾重在“承諾”，適用于數據屬主向第三方證明承諾中的敏感數據滿足一定的約束關系，由于不直接提供解密功能，不能直接支持需要互不透露敏感數據明文的多方協同計算，這一點與密碼學領域的同態加解密算法有很大區別，切勿混淆概念。

3.量子承諾

為了應對量子計算可能帶來的風險，尋求經典密碼學承諾技術的替代品，后量子密碼學承諾也是重要的研究方向之一。比較典型的方案有量子比特承諾。

量子比特承諾(QuantumBitCommitment)是基于量子力學原理構造的比特承諾方案，具體實現可以抽象為一個帶隨機輸入的單向哈希算法。

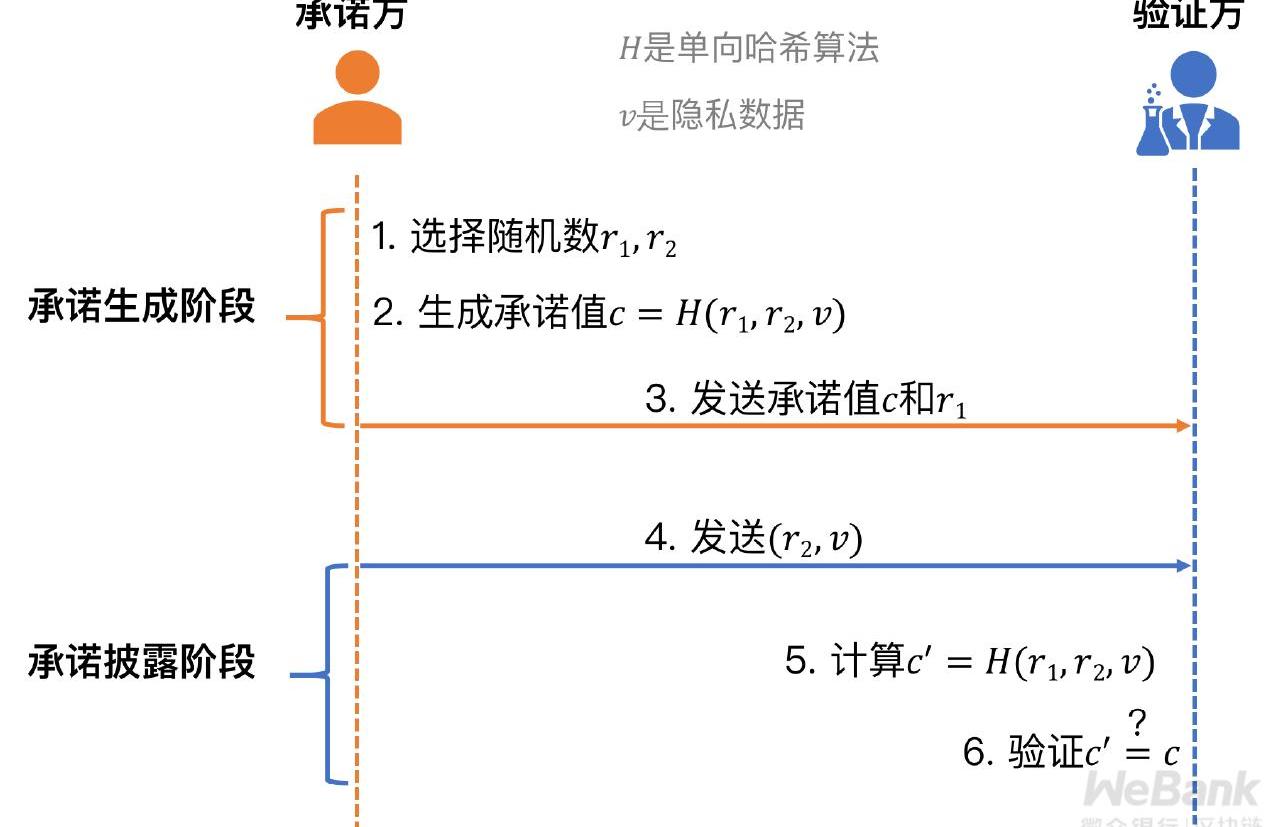
根據單向函數的單向性，承諾方向驗證方發送r1和c后，驗證方不知道v，滿足對v的隱匿性。另外，由單向哈希的抗碰撞性可知承諾方難以找到r2′和v’，使H(r1,r2,v)=H(r1,r2′,v′)，因此承諾方難以違約，滿足對v的綁定性。

量子比特承諾的構造看似簡單，但實際實現需要借助量子協議完成計算，同時也有一定的理論局限性。

早在1996年，Hoi-KwongLo和HoiFungChau團隊、DominicMayers團隊分別獨立地證明了不存在滿足信息論安全的理論最強綁定性的量子比特承諾方案。這個不存在性被稱為MLCno-go定理。其主要原因是，如果驗證方完全沒有任何承諾的信息，那么承諾方可以通過量子糾纏隨意地改變承諾內容，而驗證方既不能阻止也不能發現承諾方的違約行為。

總體而言，后量子密碼學承諾的研究尚處于早期階段，充滿了各類挑戰，目前難以直接應用到實際業務系統中。除了量子比特承諾之外，基于模糊算法的量子模糊承諾也是一類熱門研究方向，目標應用領域為生物特征識別相關的隱私安全系統。將來不排除有更實用的方案面世，以此消解量子計算可能帶來的沖擊，我們將持續保持關注。

正是：業務數據精確至毫厘，密碼承諾隱匿遁無形！

密碼學承諾的隱匿性和綁定性是隱私保護方案設計中常用的關鍵特性，在保障隱私數據機密性的同時，也保證了密文形式隱私數據解讀的唯一性。對于業務系統設計而言，密碼學承諾為隱私數據提供了另一種高效的密文表達方式。

本論中，我們重點介紹了哈希承諾和Pedersen承諾，在往后的文章中，我們還會進一步介紹其他重要的密碼學承諾，例如zk-SNARKs零知識證明系統中使用的多項式承諾、向量承諾等。

對于需要在數據的密文形式上直接進行運算和交叉驗證的業務，只要不涉及互不透露數據明文的多方協同計算，相比現有同態加密算法，以Pedersen承諾為代表的密碼學承諾往往可以提供更好的性能。這一優勢與密碼學承諾的同態性密不可分，如何構造和應用同態性，敬請關注下文分解。

Tags：SENEDE比特幣區塊鏈SENC幣Zeedex比特幣最新價格行情美元銀行區塊鏈幣有什么用

Uniswap