Nothing:為了解決這個問題，大名鼎鼎的數學家不惜……

本文轉自：科普中國

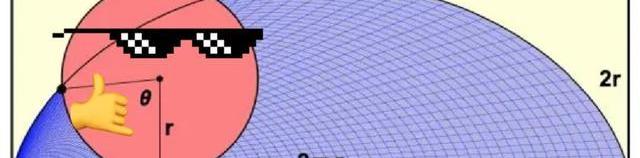
最近我學習了一種新的曲線——旋輪線，來和我一起看看吧，你也會覺得很驚奇的。

我想我們所認識的大多數形狀都時不時地出現在日常生活，很難發現新的形狀。從小學起我們就已經認識了方形、圓形和三角形，后來又學習了雙曲線、橢圓還有正弦曲線，但很多人都不知道這個形狀……那就是我最近才發現的令人驚奇的——旋輪線。接下來我將與大家一起學習這個新形狀。

什么是旋輪線？

在維基百科中，旋輪線被定義為“一個圓無滑動地沿一條直線滾動時，其邊上一點運動的軌跡。”用下面這個動圖展示可能會更加直觀一些：

伊安布利霍斯是古希臘哲學家、長袍潮流引領人，也是旋輪線的發現者，顯然旋輪線帶來的名氣不能讓他擁有自己的半身大理石像。

我想包括我在內的大多數人也只是知道伽利略是最早研究旋輪線并給它起名的人，他甚至用金屬板制作了旋輪線的模型來研究旋輪線下的面積。如果那時候有微積分的話或許就容易一些了吧。順便一提，發明水銀氣壓計的托里拆利才是最終求解單條旋輪線下面積的人。

隨著時間推移，旋輪線吸引了大批有名望的數學家，其中包括笛卡爾、費馬、帕斯卡、牛頓、萊布尼茨、洛必達、伯努利、歐拉、拉格朗日等等我能一下子就叫上來的名字。

他們顯然很喜歡創造一些關于旋輪線的競賽和問題，之后再以相互攻擊和辱罵結束。

帕斯卡早先就創造了一個關于求解旋輪線的重心、面積以及體積的比賽，并以西班牙金幣作為獎金。可惜，三位評審認為沒有人獲勝。倫敦的圣保羅大教堂的設計者克里斯托弗·雷恩遞交了一份關于計算旋輪線長度的證明，雖然這不是競賽的內容，但仍值得贊許。一位評委在多年后聲稱自己已經解決了這個問題但一直沒有文字記載，于是引發了輿論戰爭。

日本央行副行長若田部昌澄：日本央行實施貨幣寬松政策不僅是為了推高價格，也是為了實現經濟的良性循環:2月3日消息，日本央行副行長若田部昌澄：日本央行實施貨幣寬松政策不僅是為了推高價格，也是為了實現經濟的良性循環，即價格上漲伴隨著工資、收入和就業增加。[2022/2/3 9:28:44]

遺憾的是，伯努利在1696年提出的挑戰最終也以失敗告終，之后我會給大家介紹。

利用數學更深入地了解旋輪線

我們已經對旋輪線的歷史有所熟悉了，你可能會有些和偉人伽利略、雷恩一樣的幾何問題：旋輪線下的面積是多少？旋輪線的長度是多少？旋輪線到底是什么形狀的啊？

還好我們有數學和發達的網絡。

下面的參數方程可以表示出在一個圓前進時上面一點隨時間變化的用x、y坐標表示旋輪線軌跡，x、y彼此獨立，所以有兩個方程：

x(t)=r(tsin(t))

y(t)=r(1cos(t))

為了更好地理解這兩個方程，我們令t=π.此時x(π)=r(πsin(π))=r(π0)=πr.因為圓的周長為2πr，此時圓滾動了半圈；這個點的高度為y(π)=r(1cos(π))=r(1+1)=2r，兩倍的半徑可以看出圓上這一點達到了滾動一周的最高點。

通過兩個等式，我們就可以利用微積分來計算旋輪線的長度和面積了。利用網絡的幫助和對早先數學知識的回憶，我利用不同顏色的筆完成了這個優雅的證明：

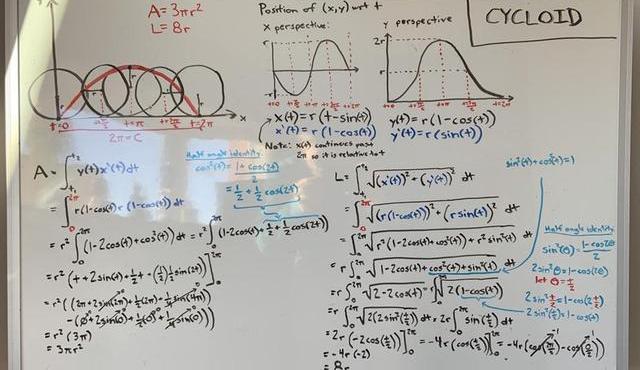
就像有關于圓的其他問題一樣，這個解非常簡潔，單條旋輪線下的面積是3πr.令人驚奇的是，伽利略對于旋輪線下面積和圓面積的比值計算已經非常接近3:1了，而這個結果只是用非常老派的金屬拼接方法來完成的。旋輪線的長度是8r，和雷恩老早就算出來的一致，之中沒有π的影子。

美聯儲博斯蒂克：為了抗擊通脹，需加息三次并迅速縮表:1月11日消息，美聯儲博斯蒂克表示，由于通脹偏高且經濟復蘇強勁，美聯儲今年將至少需要加息三次，最快從3月開始，同時也有必要迅速縮減美聯儲資產持倉，藉以將金融體系內過多的現金抽離。博斯蒂克周一在接受采訪時表示，他不認為新一波疫情爆發將會拖累復蘇，反而是認為這更有可能使通脹加劇，導致2022年有必要第四次加息25個基點，而不是放慢腳步并讓美聯儲有喘息空間。博斯蒂克今年沒有貨幣政策投票權，他是首批預計復蘇步伐將強于預期的美聯儲官員之一。一年前，他是少數幾個預計2022年加息的官員之一。 （金十）[2022/1/11 8:41:41]

這個結果可以說非常之優美。

物理中的旋輪線

旋輪線只是中看不中用嗎？自然界中是否存在旋輪線呢？雖然不像其他幾何學親戚那樣，但旋輪線仍然以一些神奇的姿態存在于自然界中。

讓我們來回到前面提到的、伯努利在1696年向頂尖數學家們提出了他的問題：

“

我，約翰·伯努利，致全世界最聰慧的數學家們：

對于聰明的人們來說，沒有什么比一個直白且具有挑戰性的問題更具有吸引力的了，更別說這些解法可能會讓他們聲名鵲起，流芳百世。根據帕斯卡、費馬等人提出的例子，我希望我也能通過提出一個現在最頂尖的數學家們考驗自己頭腦的技巧和力量的問題，來獲得學界的感謝。如果有人能夠給出我接下來的問題的解法，那么我將在公眾面前表達對他的贊美。

這個人完全不認為自己在說大話——雖然“公開贊揚”聽起來好像并沒有西班牙金幣有吸引力。接下來就是他的問題：

“

在一個垂直空間中有點A和點B，有一質點只受到重力的作用從A至B，它的軌跡經過什么樣的曲線用時最短？

換句話說，如果有一個小球只受重力場的作用，在一個無摩擦力的軌道上從高一點的A點至低一點的B點運動，那么什么軌跡可以使小球運動的時間最短？

DeFi Pulse創始人：為了自身安全不會與1inch團隊進行互動:2月9日晚間，DeFi分析平臺DeFi Pulse創始人Scott Lewis在推特上表示：“1inch創始人因以下原因被永久禁止進入我們的空間。1.對我的身體暴力威脅；2.謊稱我們團隊的一名成員是罪犯，并聲稱他們馬上就會被逮捕。3.多次騷擾團隊成員。4.1inch.exchange）多次違反了禁止聯絡的要求，歡迎任何社區成員在DeFi Pulse列表上維護1inch，但為了自身安全，我們不會與1inch團隊進行互動。”此前早些時候，1inch.exchange官方推特指責Scott Lewis忽略了他們的項目。[2021/2/10 19:22:30]

但考慮到伯努利用錯誤的方法推導出了正確的結果、又從自己的兄弟那里抄來了正確的推導，他的“獎勵”變得有趣了不少。

伯努利給公眾了六個月的時間去提交解答，但沒有收到回應。萊布尼茨提議將提交的期限延長至一年半，在這個延長期里，牛頓完成了這個挑戰。

據牛頓說，他是在1967年1月29日下午4:00從皇家鑄幣廠回家時收到的約翰·伯努利的信件的。他工作了整晚并在第二天以匿名的方式郵出了自己的正確解答，但由于這個解答太過于優秀、太過于“牛頓”，伯努利一下子就認出了“留下這個爪印的獅子”。

牛頓一晚上的解決時間打破了伯努利所用的兩周的記錄。牛頓在自己的信中加入了一些當時數學家愛表達的不屑：“我不喜歡被外國人在數學方面糾纏和取樂……”牛頓從來都不怎么討人喜歡，可以說是不近人情。

牛頓，最不近人情的旋輪線數學家。

這個牛頓和伯努利解出的最快路徑被稱為最速降落曲線，來源于希臘語中的“最短時間”，根據這篇文章的主題相信大家也猜到了，這個路徑就是旋輪線的一段，下面的動圖用實驗來展示這個問題：

OKEx CEO：Libra單貨幣穩定幣計劃僅是為了加快著陸速度，而不是為了加密:OKEx CEO?JayHao今日在推特轉發Libra協會推出單貨幣穩定幣的內容，并評論稱，現在的Libra僅僅是一個由單一法定貨幣支撐的穩定幣體系，不再沒有許可。這個妥協僅僅是為了加快Libra的著陸速度，而不是為了加密。[2020/4/17]

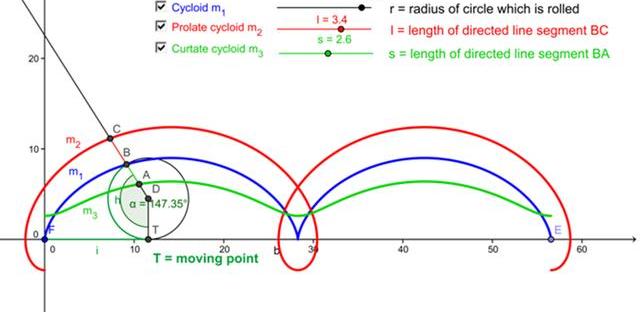
不同的旋輪線曲線。

接下來我們可以看到由滾動的圓形或其他圖形繞某些圖形所組成的旋輪線家族。

你也可以通過從任意高度掉落物體來創造一條旋輪線，這個物體相對于地球的下落軌跡是一條豎直的線，但由于地球是一個旋轉的圓形，所以這個下落軌跡將會是一條輕微的倒旋輪線！

文學中的旋輪線

在過去幾個世紀中的文學作品中偶爾露面的旋輪線一定小有名氣，雖然我不能列出所有的情況，但以下是從赫爾曼·梅爾維爾在1851年的經典作品《白鯨》中的一段：

“

在“裴闊德號”左手邊的煉鍋里，隨著滑石在周圍不住地繞圈，我突然第一次間接意識到一個事實，那就是所有在旋輪線上滑動的物體，以我的滑石為例，對于幾何學來說，無論之前在哪一點，之后都會一同落下。

建筑中的旋輪線

可以看出旋輪線真的很有意思，我在想是不是在日常生活中還遺漏了一些旋輪線。

建筑由大量的幾何圖形組成。許多著名的拱都來源于圓形、橢圓形、拋物線型以及懸鏈線。每種都有大量的例子，我從中挑選了幾個非常有名的：

聲音 | 美國國會議員：提交SEC交易法是為了讓美國再次在創新領域取得領先:據cryptodaily消息，美國國會議員Darren Soto和Warren Davidson提請了一項修改申請，旨在調整執行了七十余載的證券法以適配當前的加密貨幣市場。Davidson以互聯網初期發展為類比表示，在互聯網發展初期，國會通過立法提供了監管確定性，并降低了過度監管對市場的傷害。我們的目的是為了讓美國經濟在這個創新領域再次取得領先。[2018/12/21]

巴黎的凱旋門是半圓拱券，也被稱為古羅馬拱券。

跨過倫敦泰晤士河的邱橋具有半橢圓拱，能夠為船只和火車等交通工具創造較寬闊的跨度。

加州大蘇爾美國一號公路的比克斯比橋具有拋物線拱。攝影：Alamy。

密蘇里州圣路易斯的拱門是一個懸鏈線拱，由于重量分布均勻，是最堅固的拱形。

旋輪線看起來和拱很相似，所以有沒有建筑用旋輪線拱的呢？根據網上的搜索結果，是有的，只是很少。有兩個例子在介紹中反復出現：

第一個是美國德州沃斯堡的金貝兒藝術博物館的屋頂，這個屋頂上的多個拱形是由一系列間隔的旋輪線組成的，這個滾輪構成的圖形給予了它平滑的外觀，非常適合一個藝術博物館。

德克薩斯沃斯堡，金貝爾藝術博物館的旋輪線拱。

第二個擁有旋輪線拱的建筑是達特茅斯學院中霍普金斯中心正面的拱，是我本科就讀的學校，這讓我產生了另外的思考：是不是我四年中每天都看到這個建筑，才為旋輪線如此著迷？

新罕布什爾州漢諾威，達特茅斯學院的霍普金斯中心正面的旋輪線拱。

藝術和娛樂中的旋輪線

可能你小的時候就已經“玩”過旋輪線了。萬花尺是基于一種被稱為內旋輪線的一般旋輪線的玩具，不同于隨直線滾動的圓，內旋輪線是“由附著在大圓內滾動的小圓上一定點的軌跡構成的特殊平面曲線”。

萬花尺。

內旋輪線有兩個特殊形式三角旋輪線和星狀線，可以分別通過特定的小圓沿大圓內部滾動三周及四周獲得。你可能會在一些標識上見過星狀線。

匹茲堡鋼人橄欖球隊的標識上包含3個星狀線。

如果你覺得這種線條很令人舒適，有一些藝術家會利用多個不同尺寸組合滾動的圓來創造旋輪線藝術：

在Pinterest上的旋輪線藝術裝置。

Kickstarter上售賣的旋輪線藝術品。

光學中的旋輪線

另一種旋輪線形式可以通過沿一個圓外部滾動的圓上一定點的軌跡構成。有一個特別的例子是心臟線，是一個圓沿另一個半徑相等的圓外運動其上一點的軌跡構成的圖形，如下圖所示，這個形狀剛好有一個尖角類似于一顆心，也是它名字的來源：

下次早晨喝茶的時候一定要瞪大眼睛看看茶杯里的圖形！

分形幾何和混沌理論的框架曼德勃羅集合的中心區域的邊界也是一個精確的心臟線，雖然我不知道具體的原因，但仍然是另一種心臟線表現形式。

曼德勃羅集合第一階段的中心區域由一個完美的心臟線圍成。

旋輪線的形狀不止局限于圓形，你也可以沿一條直線滾動一個非圓形然后發現一個全新的圖形——多邊形轉跡線，下面是三角形和方形滾動的轉跡線：

木星的衛星歐羅巴表面的旋輪線形。

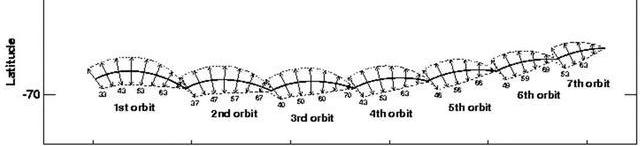
歐羅巴表面的旋輪線形成。

總結

我希望你也從這篇文章中學到一些新圖形的知識，畢竟旋輪線是一群很有意思的圖形，在我看了一系列的旋輪線后，更想去深入認識身邊的宇宙了……

參考文獻：

Eli,MaorandEugenJost.“TwistedMathandBeautifulGeometry.”AmericanScientist.

Lynch,Peter.“Thecurvedhistoryofcycloids,fromGalileotocyclegears.”TheIrishTimes.17-Sep-2015.

作者：RySullivan

翻譯：zhenni

審校：Nothing

原文鏈接：

https://medium.com/@rysullivan/celebrating-the-cycloid-be4350ff187b

翻譯內容僅代表作者觀點

不代表中科院物理所立場

編輯：zhenni

來源:中科院物理所

Tags：NothingNothing幣是什么幣

中幣下載