區塊鏈:密碼學研究 | 動手計算雙線性對（上）

零知識證明是重要的密碼學技術之一，其中基于電路的通用零知識證明算法更是因為近年取得的長足發展和在區塊鏈項目中的應用而備受關注。雙線性映射，也叫雙線性配對或雙線性對，是通用零知識證明算法的重要組成部分，也是眾多密碼體制，如聚合簽名、身份基加密、屬性基加密等的關鍵構件。本文從零基礎開始，通過完整的模擬雙線性對的原理來實現一套在小有限域上的雙線性映射，幫助讀者加深對雙線性映射的理解。

“動手計算雙線性對”這個系列計劃有上中下三篇內容，本文是上篇，介紹后面文章需要的一些基礎知識。在中篇，我們將對一個名為curve101的曲線進行討論，其有限域只涉及101個元素，用于配對的橢圓曲線子群只有17個點，不借助計算機也能方便的通過純手算完成整個過程，十分適合零基礎讀者入手。下篇則會實際計算并討論雙線性對的實際例子，全部的中間計算過程我們都將列出，讀者可以按步驟重現整個計算流程。

在之后介紹零知識證明算法的系列文章中我們還會用到這個curve101進行演示，屆時讀者可以更加明白雙線性對的作用，而接下來我們就來一起從零基礎開始演算這個雙線性曲線。

Mano 首席技術官：Web3 的額外部分是對等發現層、密碼學和共識協議:金色財經現場報道，在Coinlive舉辦的峰會上，題為“塑造新加坡數字資產類別的未來”的圓桌討論邀請了 Cobo 首席運營官 Lily Z. King、新加坡管理大學 (SMU) 經濟學助理教授（實踐） Goh Jing Rong、Immin Mano Thanabalan 首席技術官、德國創業亞洲 Yitch，區塊鏈協會 (BAS) 合作伙伴總監 Yoon KC (Steven)。關于 Web3 是什么以及數字資產在 Web3 生態系統中扮演什么角色的問題，Mano 首先說 Web3 的額外部分是對等發現層、密碼學和共識協議，這可能是最有趣的。 YC 澄清應該是 Web3 而不是 Web 3.0。

Lily 補充說，EWeb3 有望成為一個更加開放的互聯網，讓所有用戶都能從中受益。 Jing Rong 列出了下一代互聯網的三個定義，使用新聞技術來改進當前的網絡，并專注于去中心化，即控制權被分配給生態系統中的多方。最后一個給出答案的 Yitch 解釋說，歸根結底，數字資產只是數字，除非你可以創造現實世界的效用。其他問題，如數字資產的機構采用、法規等，引起了小組成員的不同回應。[2022/12/22 22:00:54]

眾所周知，很多公鑰密碼體制都是建立在有限域上，特別是模素數的有限域。作為零基礎的系列，我們不去糾結數學概念“域”的嚴格定義，而是通過介紹帶模運算相關的內容，來真實的展現一個有限域。

上海市數據隱私安全計算企業重點實驗室參與完成論文被密碼學頂級會議PKC收錄:近日，上海市數據隱私安全計算企業重點實驗室謝翔博士聯合香港大學學者共同合作的論文《Compact Zero-Knowledge Proofs for Threshold ECDSA with Trustless Setup》被公鑰密碼學領域國際頂級會議PKC 2021錄用，該會議將在北京時間2021年5月9日至13日于線上舉行。PKC是國際密碼學會（IACR）主辦的專注于公鑰密碼學方向的旗艦會議，每一年舉辦一次，今年是第24屆，該會議一直是學術界和工業界共同關注的焦點。

本次上海市數據隱私安全計算企業重點實驗室參與完成的論文亮點在于零知識證明（ZKP）方向的研究。在理論層面，我們提出的零知識證明包括HSM群中的離散對數關系和Castagnos-Laguillaumie（CL）密文的格式良好性。在實際應用層面，我們利用零知識證明改進了兩方ECDSA和門限ECDSA的性能。

上海市數據隱私安全計算企業重點實驗室以矩陣元科研中堅力量為基礎，匯集國內密碼學專家、學者組建而成。研究內容為針對數據融合與協同計算基礎設施建設過程中保護數據安全與隱私的基礎理論技術。[2021/4/7 19:55:55]

帶模運算是在我們熟悉的加法和乘法的基礎上增加一步計算余數的操作，例如，在以7為模數的系統中：

林煌博士：輕模式的隱私應用是密碼學技術在隱私保護實踐中很重要的一步:在今日的《金色深核》線上直播中，針對“假設我們要解決多公司之間數據需要保密且共同使用的問題，三個技術路線如何去做？去年Maskbook火了一下，各位如何看待這種“輕模式”的隱私應用？”Suterusu林煌博士表示關于多個公司之間進行保密數據的安全計算，這個需要結合零知識證明和安全多方計算才能解決。如果我們考慮一種簡單的情況，只有兩方進行安全計算，一方可以將自己的數據用門限同態加密方案的公鑰加密后傳輸給另一方，另一方依據加密自己的數據生成密文，然后在兩個密文上做預定的同態運算，最后雙方合作把完成同態操作的密文解密。零知識證明可用于保證這個過程的計算可靠性（computational integrity），比如如何保證生成的加密密文確實是按照正確加密步驟生成的密文且加秘方知道原始明文呢？我們可以使用零知識證明算法針對加密電路生成能夠驗證明文和密文之間符合加密電路邏輯的證明。輕模式的隱私應用毫無疑問是密碼學技術在隱私保護實踐中很重要的一步，但這個領域還有很多可以做的事情。[2020/3/11]

3+3=6，也就是mod7=6

聲音 | 楊慶峰：現代密碼學結合區塊鏈技術可基本消除技術層面的安全問題:據澎湃新聞消息，上海大學哲學系教授楊慶峰發文指出，如果說長三角一體化建設過程中數據共享會成為一個問題，數據共享會影響到未來長三角一體化公共服務的落實，那么這個問題就必須嚴肅對待。同時，其表示現代密碼學的方法已完全可以解決這一問題，再加上區塊鏈技術的未來運用的可能性極大，這基本上消除技術層面出現的安全問題。需要擔憂的是倫理方面的問題，諸如隱私保護、被遺忘權等方面的問題。[2019/3/14]

3+6=2，也就是mod7=2

4×2=1，也就是mod7=1

所謂模素數就是說取模操作針對的是某個素數p，例如上述的7，或者curve101中的101。p是素數這個細節是關鍵的，在下文介紹帶模乘法的逆運算時你將會對這一點的必要性有更深的體會。

有了模加法，我們可以定義其逆運算是模減法，例如：

6-3=3，也就是mod7=6

金色財經現場報道 String Lab聯合創始人兼CEO丁磊：區塊鏈的左手是密碼學家，右手是經濟學家:金色財經現場報道，今日粵港澳大灣區新金融論壇上，String Lab聯合創始人兼CEO丁磊分享對于區塊鏈的思考中提到，區塊鏈正在改變生產關系，其中，密碼學家是左手，經濟學家是右手。經濟學家也就是機制的制造者，通過代幣等級制，把更大的生產網絡聯系在一起，讓人們為各自的利益服務的情況下，創造新的生態系統。[2018/4/7]

2-6=3，也就是mod7=3

同理，有了模乘法，自然而然會想到去定義其逆運算“模除法”。但是加、減、乘我們可以直接正向計算得到，“模除法”就比較困難。例如為了求3/2等于幾必須思考哪個數乘以2等于3，而這個思考過程并不是特別直接。好在我們模7的例子中涉及到的元素并不多，因此通過窮舉就能找到答案：因為2×5=3，所以3/2等于5。

需要注意到3/2其實可以轉化為3×(1/2)，而因為剛才我們計算過4×2=1，所以1/2的值我們其實是知道的。因此3/2=5可以通3×4=5計算出來。這啟發我們可以枚舉全部形如1/n的數得到一個“倒數表”，然后借助“倒數表”將除法轉化為乘法進行。

模7逆元表

按習慣，我們一般不用1/n的寫法，也不用“倒數”這個稱呼。而是將1/n寫做?n-1，并將其稱為n的逆元。下文我們將遵從習慣，使用逆元這個叫法。顯而易見的是，在不同的模系統中，同一個數的逆元是不同的。比如模7系統中，3的逆元是5；而模11系統中3的逆元是4。因此除非有明確的語境和上下文，否則為了避免歧義，還要說明逆元是模幾的逆元才有意義，比如一個完整的說法是：3的模7逆元是5。

在模7的系統中，我們為每個元素都找到了逆元，在模17和模101的系統中也可以完成這樣的操作。那么我們自然而然會想：是否在任何模的情況下都能為每個元素找到逆元呢？答案是否定的，例如在模8的系統中，找不到任何一個數乘以2等于1，也就是說在模8的系統中計算1/2這個“除法”是沒有意義的。實際上，只有在模為素數的情況下才能為每個元素都找到逆元，也就是說在模素數的情況下我們才可以給任意兩個元素計算“除法”。在這樣的模素數系統中，任意兩個元素都能完成加減乘除四則運算，我們稱模7加法、模7乘法和集合{0,1,2,3,4,5,6}組成一個有限域：模7剩余類域。

所謂“有限”的意思就是集合的元素是有限的，比如這里的7個元素。雖然在本篇科普性質的文章對待數學概念都并非十分嚴格和謹慎，但是這里仍然能夠揭示域的一些關鍵性質。比如我們發現僅利用集合中的元素就能夠計算四則運算。模7剩余類域是這樣，有理數域、復數域等也都是這樣，意識到這一點就已經足夠完成后面文章的閱讀了。我們后面用Fp代指模p剩余類域，例如F7，F101等。

討論完了加減乘除四則運算，按照我們曾經學習有理數的思路，我們來考慮開平方運算。例如3×3mod7=2，所以3是2的“平方根”。如果某個非零元素是可以開平方根的，我們稱這樣的元素為模7的二次剩余，否則就叫模7的二次非剩余。這樣我們可以列出下面一張表：

可以注意到，二次剩余的個數和二次非剩余的個數是相等的，二次剩余的逆元仍然是二次剩余，二次非剩余的逆元也仍然是二次非剩余；而且我們還注意到，每個二次剩余都有兩個根并且他們的和為0，這一點性質像極了正實數：正實數的平方根總有兩個，他們互為相反數。

如何判定一個數是否為二次剩余和如何求二次剩余都是有趣和實用的問題。比如在動手計算雙線性對會談到的橢圓曲線中，已知x坐標和橢圓曲線方程求y的過程就需要考慮計算二次剩余的問題。相關的方法一般會涉及到勒讓德符號等。而在我們的討論的例子中因為元素的數量很少，我們一般采用窮舉的方法就能解決。

經過上面的演算，我們發現3在F7中沒有“平方根”，也就是不存在某個數其平方模7為3。類比復數域對實數域的擴展，我們假設3的一個平方根為j，即j*jmod7=3。現在我們把j加入到{0,1,2,3,4,5,6}集合中，然后嘗試再加入一些其他元素使得新的集合仍然構成一個域。

首先為了能夠計算加法和減法，至少還要加入j、1+j、2+j、3+j、4+j、5+j、6+j，為了能夠計算乘法我們至少還要加入j、2j、3j、4j、6j、6j，最終我們發現一個新的能夠計算四則運算的集合至少要有下面49個元素：

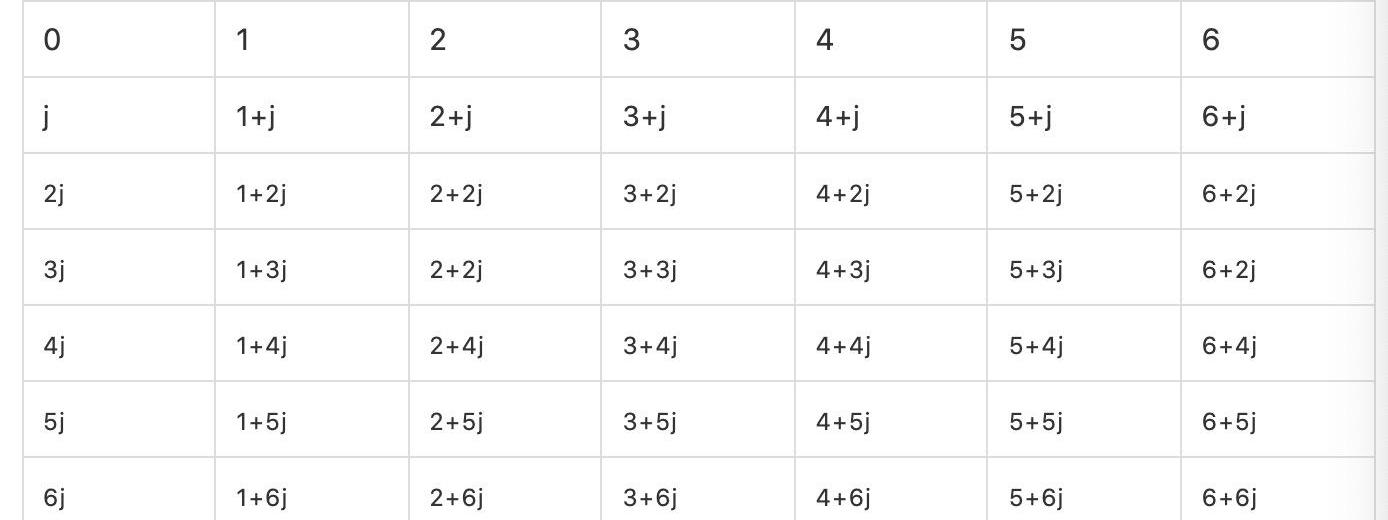
例如6j+j=0；(3+j)(5+2j)=4j;(4+4j)-1=6-6j

那么僅用這49個元素能夠完成四則運算嗎？答案是肯定的，雖然本文不去嚴格證明這一點，但是可以簡單揭示一些其中的原因：

對于加法和減法，我們很容易驗證任意兩個元素的和、差都在還在集合中；對于乘法，因為j×j=3這條規則，簡單驗證后我們就能發現任何兩個元素的積還是在集合中；唯一需要仔細考慮一下的是除法；對于除法，我們總可以通過如下方式計算a+bj的逆元：

因為a和b是F7中的元素，因此a2-3b2?也是F7中的元素，因此可以判定a2-3b2?的逆元仍然是{0,1,2,3,4,5,6}中的元素。所以最后可以發現a+bj的逆元是(a-bj)(a2-3b2)-1，它仍然落在49個元素之中。所以新的49個元素組成的集合不但包含{0,1,2,3,4,5,6,j}，而且能夠計算四則運算。這個新的集合其實也是一個有限域，我們稱其為F7的二次擴域，記為F72，之所以是“二次”，我們可以這樣粗暴的理解：每個F72中的元素需要兩個F7的元素通過組合的方式來表示。

本篇介完了關于模運算和模p剩余類域的一些基礎知識，下一篇“動手計算雙線性對”，我們會介紹關于有限域上橢圓曲線的一些例子和知識，屆時會使用到本篇中的內容，敬請期待。

作者簡介

喬沛楊趣鏈科技基礎平臺部區塊鏈底層密碼學小組

Tags：區塊鏈WEBMODWEB3區塊鏈幣種類WEB幣mod幣圈是什么意思web3游戲行業

Ethereum