HASH:一文讀懂Schnorr簽名如何提升比特幣

原文標題：《干貨 | Schnorr 簽名如何提升比特幣》，作者Stepan

在閱讀 Blockstream 撰寫的?MuSig?論文時，我一直在想象，這對于我一個比特幣用戶來說，到底意味著什么。我發現 Schnorr 簽名的一些特性實在是非常棒而且便利，但某一些特性則非常煩人。在這篇文章里，我希望能跟各位分享我的想法。不過，我們先快速回顧一下。

當前比特幣的所有權體系用的是?ECDSA（橢圓曲線簽名算法）。在簽名一條消息?m?時，我們先哈希這條消息，得出一個哈希值，即?z = hash(m)?。我們也需要一個隨機數（或者至少看似隨機的數）k?。在這里，我們不希望信任隨機數生成器（有太多的錯誤和漏洞都與不合格的隨機數生成器有關），所以我們通常使用?RFC6979，基于我們所知的一個秘密值和我們要簽名的消息，計算出一個確定性的 k。

使用私鑰?pk?，我們可以為消息?m?生成一個簽名，簽名由兩個數組成：r（隨機點?R = k * G?的 x 坐標）和?s = (z + r*pk)/k。

然后，使用我們的公鑰?P = pk * G?，任何人都可以驗證我們的簽名，也就是檢查?(z/s)×G+(r/s)×P?的 x 坐標確為?r。

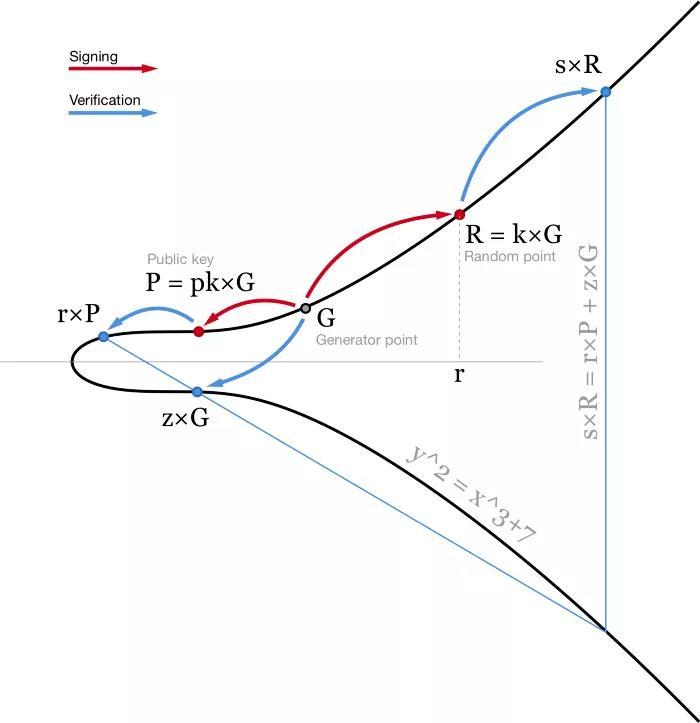
ECDSA 算法圖解。為便于說明，橢圓曲線作在實數域上?

這種算法是很常見的，也非常好用。但還有提升空間。首先，簽名的驗證包含除法（1/s）和兩次點乘法，而這些操作的計算量都非常大。在比特幣網絡中，每個節點都要驗證每一筆交易，所以當你在網絡中發出一筆交易時，全網幾千個節點都要驗證你的簽名。因此，即使簽名的過程開銷變得更大，讓驗證簽名變得更簡單也還是非常有好處的。

安全團隊：1Minute Alpha Discord及“1Minute MINT LIVE NOW”推特賬號遭到攻擊:金色財經消息，據CertiK監測，1Minute Alpha項目Discord服務器以及“1Minute MINT LIVE NOW”推特賬號遭到攻擊。請社區用戶在頻道修復之前不要點擊其發布的任何鏈接。[2022/12/14 21:43:43]

其次，節點在驗證簽名時，每個簽名都要單獨驗證。在一個 m-n 的多簽交易中，節點必須多次驗證同一個簽名。比如一筆 7-11 的多簽名交易，里面包含了 7 個簽名，網絡中的每個節點都要分別驗證 7 個簽名。另外，這種交易的體積也非常大，用戶必須為此付出多得多的手續費。

Schnorr 簽名的生成方式有些許不同。它不是兩個標量?(r, s)，而是一個點?R?和一個標量?s?。類似于 ECDSA 簽名，R 是一個橢圓曲線上的隨機點?R = k * G。而簽名的第二部分 s 的計算過程也有一些不同：?s = k + hash(P,R,m) ? pk?。這里 pk 就是你的私鑰，而?P = pk * G?是你的公鑰，m 就是那條消息。驗證過程是檢查?s * G = R + hash(P,R,m) * P。

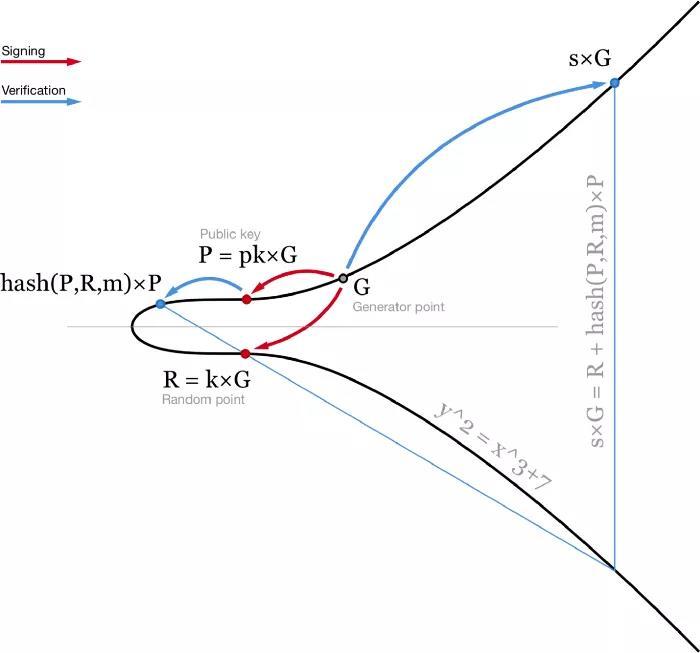
圖解 Schnorr 簽名和驗證?

這個等式是線性的，所以多個等式可以相加相減而等號仍然成立。這給我們帶來了 Schnorr 簽名的多種良好特性。

RTFKT：正準備Clone X的鑄造網站，Clone X用戶將有一周的鑄造時間:8月31日消息，耐克旗下加密時尚潮牌RTFKT發推表示，正在準備Clone X的鑄造網站，屆時將發推宣布。如果用戶擁有一枚Clone X NFT，將有一周的時間鑄造對應NFT。[2022/8/31 13:00:24]

在驗證區塊鏈上的一個區塊時，我們需要驗證區塊中所有交易的簽名都是有效的。如果其中一個是無效的，無論是哪一個 —— 我們都必須拒絕掉整個區塊。

ECDSA 的每一個簽名都必須專門驗證，意味著如果一個區塊中包含 1000 條簽名，那我們就需要計算 1000 次除法和 2000 次點乘法，總計約 3000 次繁重的運算。

但有了 Schnorr 簽名，我們可以把所有的簽名驗證等式加起來并節省一些計算量。在一個包含 1000 筆交易的區塊中，我們可以驗證：

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

這里就是一連串的點加法（從計算機運算的角度看，簡直是免費的）和 1001 次點乘法。已經是幾乎 3 倍的性能提升了 —— 驗證時只需為每個簽名付出一次重運算。

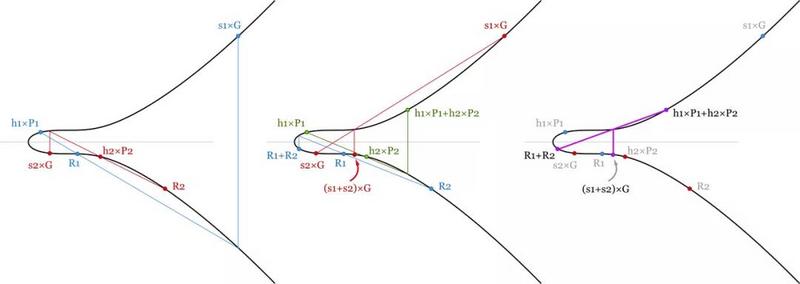
兩個簽名的批量驗證。因為驗證等式是線性可加的，所以只要所有的簽名都是有效的，這幾個等式的和等式也必成立。我們節約了一些運算量，因為標量和點加法比點乘法容易計算得多。

Cashfree推出提供卡代幣化互操作性的解決方案“Token Vault”:6月29日消息，支付提供商Cashfree Payments周三宣布其代幣化解決方案“Token Vault”將提供卡代幣化的互操作性。Token Vault的互操作性特性將幫助使用多個支付網關的企業通過其選擇的任何支付網關和卡網絡處理代幣化卡交易。

使用Cashfree支付網關的企業可以與Token Vault集成，以安全地代幣化所有主要卡網絡發行的卡，包括RuPay、Visa和萬事達卡。藉由此功能，企業將不再需要花費時間與多個代幣服務提供商集成來代幣化卡和執行交易。（The Economic Times）[2022/6/29 1:39:12]

我們想要安全地保管自己的比特幣，所以我們可能會希望使用至少兩把不同的私鑰來控制比特幣。一個在筆記本電腦或者手機（在線錢包，熱錢包）上使用，而另一個放在 硬件錢包/冷錢包 里面。即使其中一個泄露了，我們還是掌控著自己的比特幣。

當前，實現這種錢包的做法是通過 2-2 的多簽名腳本。也就是一筆交易需要包含兩個獨立的簽名。

有了 Schnorr 簽名，我們可以使用一對密鑰 (pk1,pk2)，并使用一個共享公鑰?P = P1 + P2 = pk1 * G + pk2 * G?生成一個共同簽名。在生成簽名時，我們需要在兩個設備上分別生成一個隨機數 （k1, k2），并以此生成兩個隨機點?Ri = ki * G，再分別加上?hash(P, R1 + R2, m)，就可以獲得 s1 和 s2 了（因為?si = ki + hash(P, R, m)* pki?）。最后，把它們都加起來即可獲得簽名?(R, s) = (R1+R2, s1+s2)，這就是我們的共享簽名，可用共享公鑰來驗證。其他人根本無法看出這是不是一個聚合簽名，它跟一個普通的 Schnorr 簽名看起來沒有兩樣。

美國CFTC 倡導擴大加密貨幣市場管轄范圍:金色財經報道，自比特幣創建以來已經過去了十多年，但立法者和監管機構仍在繼續探討重要問題，例如應該允許哪個監管機構來監管數字資產。包括商品期貨交易委員會 (CFTC) 在內的聯邦監管機構正在增加資源以幫助監管數字資產市場中的欺詐行為。

除了欺詐或操縱事件之外，CFTC 目前不監管涉及不依賴保證金、杠桿或融資的數字資產的現貨或現金市場交易，也不監管從事此類交易的市場參與者。然而，現任 CFTC 主席 Rostin Behnam 正在尋求擴大該機構的職權范圍。

Behnam在證詞中極力主張允許 CFTC 監管現貨數字資產交易，Behnam表示，CFTC 處于有利地位，在監管現金數字資產商品市場方面發揮著越來越重要的作用。從根本上說，CFTC 是一個市場監管機構，旨在確保市場完整性和活力，旨在支持金融穩定，同時通過基于原則的個人客戶保護監督交易所、票據交換所、數據存儲庫和市場參與者。這種靈活的方法使 CFTC 在國會授權下，與衍生品市場一起發展，從其歷史根源于監督農業市場發展到現在監督從能源和“貴金屬到金融指數和掉期。我們現在準備在數字資產商品市場上做同樣的事情。（路透社）[2022/6/22 4:43:59]

不過，這種做法有三個問題。

第一個問題是 UI 上的。要發起一筆交易，我們需要在兩個設備上發起多輪交互 —— 為了計算共同的 R，為了簽名。在兩把私鑰的情況下，只需訪問一次冷錢包：我們可以在熱錢包里準備好待簽名的交易，選好 k1 并生成?R1 = k1 * G，然后把待簽名的交易和這些數據一同傳入冷錢包并簽名。因為已經有了 R1，簽名交易在冷錢包中只需一輪就可以完成。從冷錢包中我們得到 R2 和 s2，傳回給熱錢包。熱錢包使用前述的 （k1，R1） 簽名交易，把兩個簽名加總起來即可向外廣播交易了。

Bit Digital5月份開采的比特幣減少約30%:金色財經報道，根據周三的公告，Bit Digital5月份開采了53.4個比特幣，比上個月減少了29.9%。截至5月31日，Bit Digital持有793.6BTC和316.1ETH，公允市值分別約為2520萬美元和60萬美元。截至月底，該公司擁有33,376名比特幣礦機和731名以太坊礦機——估計總哈希率分別為每秒2.17exahash和每秒0.3terahash。Bit Digital目前擁有的采礦機隊中，有17.9%部署在北美。（theblockcrypto）[2022/6/9 4:12:13]

這在體驗上跟我們現在能做到的沒有什么區別，而且每當你加多一把私鑰，問題就會變得更加復雜。假設你有一筆財富是用 10 把私鑰共同控制的，而 10 把私鑰分別存放在世界各地，這時候你要發送交易，該有多麻煩！在當前的 ECDSA 算法中，每個設備你都只需要訪問一次，但如果你用上 Schnorr 的密鑰聚合，則需要兩次，以獲得所有的 Ri 并簽名。在這種情況下，可能不使用聚合，而使用各私鑰單獨簽名的方式會好一些 —— 這樣就只需要一輪交互。

文章完成后，我得到了 Manu Drijvers 的反饋：在一個可證明安全性的多簽名方案中，你需要 3 輪交互：

選擇一個隨機數 ki 以及相應的隨機點 Ri = ki \?G，然后告訴每一個設備 Ri 的哈希值 ti=hash(Ri)，然后每個設備都能確保你沒有在知道其他人的隨機數之后改變主意*

收集所有的數字 Ri 并計算公共的 R

第二個問題是已知的 Rogue 密鑰攻擊。這篇論文講解得非常好，所以我就不贅述了。大概意思是如果你的其中一個設備被黑（比如你的熱錢包被劫持），并假裝自己的公鑰是?（P1 - P2），那就可以僅憑私鑰 pk1 便控制兩個私鑰共享的資金。一個簡單的解決方案是，在設置設備時，要求使用私鑰對相應的公鑰簽名。

還有第三個重大問題。你沒法使用確定性的 k 來簽名。如果你使用了確定性的 k，則只需一種簡單的攻擊，黑客即可獲得你的私鑰。攻擊如下：某個黑客黑入你的筆記本電腦，完全控制了其中一把私鑰（比如 pk1）。我們感覺資金仍是安全的，因為使用我們的比特幣需要 pk1 和 pk2 的聚合簽名。所以我們像往常一樣發起交易，準備好一筆待簽名的交易和 R1，發送給我們的硬件錢包，硬件錢包簽名后將 （R2, s2）發回給熱錢包 …… 然后，熱錢包出錯了，沒法完成簽名和廣播。于是我們再試一次，但這一次被黑的電腦用了另一個隨機數 —— R1' 。我們在硬件錢包里簽名了同一筆交易，又將 （R2, s2'）發回給了被黑的電腦。這一次，沒有下文了 —— 我們所有的比特幣都不翼而飛了。

在這次攻擊中，黑客獲得了同一筆交易的兩個有效的簽名：（R1, s1, R2, s2） 和 （R1', s1'，R2，s2'）。這個 R2 是一樣的，但是?R = R1 + R2?和?R' = R1' + R2?是不同的。這就意味著黑客可以計算出我們的第二個私鑰：s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))?pk2?或者說?pk2=(s2-s2')/(hash(P,R1+R2,m)-hash(P,R1'+R2,m))。我發現這就是密鑰聚合最不方便的地方 —— 我們每次都要使用一個好的隨機數生成器，這樣才能安全地聚合。

MuSig?解決了其中一個問題 —— rogue key 攻擊將不能再奏效。這里的目標是把 多方/多個設置的簽名和公鑰聚合在一起，但又無需你證明自己具有與這些公鑰相對應的私鑰。

聚合簽名對應著聚合公鑰。但在 MuSig 中，我們不是把所有聯合簽名者的公鑰直接相加，而是都乘以一些參數，使得聚合公鑰?P = hash(L,P1)×P1 + … + hash(L,Pn)×Pn?。在這里，L = hash(P1,…,Pn)?—— 這個公共數基于所有的公鑰。L 的非線性特性阻止了攻擊者構造特殊的公鑰來發動攻擊。即使攻擊者知道他的?hash(L,Patk)×Patk?應該是什么，他也無法從中推導出 Patk 來 —— 這就跟你想從公鑰中推導出私鑰是一樣的。

簽名構造的其它過程跟上面介紹的很像。在生成簽名時，每個聯合簽名者都選擇一個隨機數 ki 并與他人分享?Ri = ki * G。然后他們把所有的隨機點加起來獲得?R=R1+…+Rn?，然后生成簽名?si = ki + hash(P,R,m) ? hash(L,Pi) ? pki?。因此，聚合簽名是?(R, s)=(R1+…+Rn, s1+…+sn)?，而驗證簽名的方法與以前一樣：s×G = R + hash(P,R,m)×P?。

你可能也注意到了，MuSig 和密鑰聚合需要 *所有簽名者簽名一個交易*。但如果你想做的是 2-3 的多簽名腳本呢？這時候我們能夠使用簽名聚合嗎，還是不得不使用通常的 OP_CHECKMULTISIG 和分別簽名？（譯者注：OP_CHECKMULTISIG 是比特幣驗證橢圓曲線多簽名腳本的操作碼）

先說答案，是可以的，但是協議上將有些許的不同。我們可以開發一個類似于 OP_CHECKMULTISIG 的操作碼，只不過是檢查聚合簽名是否對應于公鑰默克爾樹上的一個元素。

舉個例子，如果我們想用公鑰 P1、P2 和 P3 組成一個 2-3 的多簽名腳本，我們需要用這幾把公鑰的所有兩兩組合 （P1, P2）、（P2, P3）、（P1, P3） 來構建一棵默克爾樹，并把默克爾樹根公布在鎖定腳本中。

在花費比特幣時，我們需要提交一個簽名和一個證據，證明這個簽名所對應的公鑰位于由這個樹根標記的默克爾樹上。對于 2-3 多簽名合約來說，樹上只有 3 個元素，證據只需 2 條哈希值 —— 那個我們想用的公鑰組合的哈希值，還有一個鄰居的。對于 7-11 多簽名腳本來說，公鑰組合有 11!/7!/4!=330 種，證據需要 8 條哈希值。通常來說，證據所包含的元素數量與多簽名的密鑰數量大體成正比 ，為?log2(n!/m!/(n-m))?。

但有了默克爾公鑰樹，我們就不必局限于 m-n 多簽名腳本了。我們可以做一棵使用任意公鑰組合的樹。舉個例子，如果我們有一個筆記本電腦，一個手機，一個硬件錢包和一個助記詞，我們可以構建一棵默克爾樹，允許我們使用 筆記本電腦 + 硬件錢包、手機 + 硬件錢包 或者單獨的助記詞來使用比特幣。這是當前的 OP_CHECKMULTISIG 做不到的 —— 除非你使用 “IF - Else” 式的流程控制來構造更復雜的腳本。

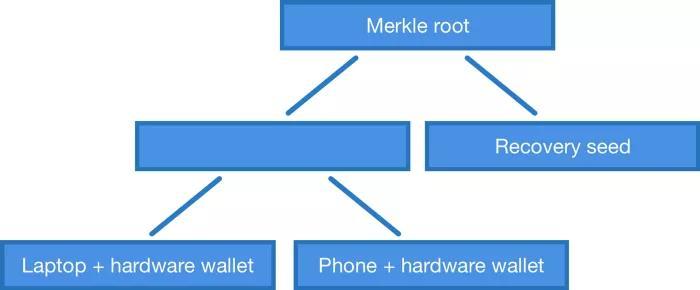
聚合公鑰的默克爾樹。不僅僅是多簽名?

Schnorr 簽名很棒，它解決了區塊驗證中的一些計算開銷問題，也給了我們密鑰聚合的能力。后者在使用時有些不便利，但我們不是在強迫大家使用它 —— 無論如何，我們都可以仍舊使用普通的多簽名方案，使用單獨的、不聚合的簽名。

我迫不及待想使用 Schnorr 簽名，希望比特幣協議能盡快納入這種簽名方案。

另外，我也真心喜歡?MuSig，它是個優雅的方案，論文也淺顯易懂。我強烈建議各位有閑之時通讀全文。

Tags：ASHHASH比特幣SCHBASHTANK幣indaHash比特幣害死多少人ccpchschain

歐易交易所app官網下載